ode-rk4

Integrate a system of ODEs using the Fourth Order Runge-Kutta (RK-4) method

Introduction

This module integrates a system of ordinary differential equations of the form

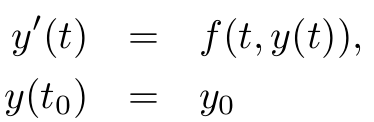
where is a vector of length . Given time step , the Runge-Kutta 4 method integrates the ODE with update

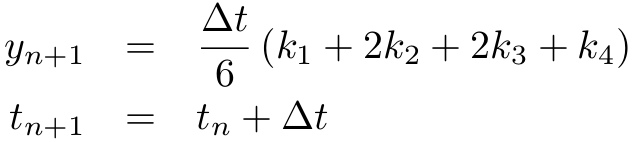
For a similar adaptive method using the fifth order Cash-Karp Runge-Kutta method with fourth order embedded error estimator, see [https://github.com/scijs/ode45-cash-karp](ode45-cash-karp].

Install

$ npm install ode-rk4

Example

var rk4 = require('ode-rk4')
 
var deriv = function(dydt, y, t) {
  dydt[0] = -y[1]
  dydt[1] =  y[0]
}
 
var y0 = [1,0]
var n = 1000
var t0 = 0
var dt = 2.0 * Math.PI / n
 
var integrator = rk4( y0, deriv, t0, dt )
 
// Integrate 1000 steps:
integrator.steps(n)
 
// Integrate all the way around a circle:
// => integrator.y = [ 0.9999999999995743, -8.160481752145232e-11 ]

API

require('ode-rk4')( y0, deriv, t0, dt )

Arguments:

• y0: an array or typed array containing initial conditions. This vector is updated in-place with each integrator step.
• deriv: a function that calculates the derivative. Format is function( dydt, y, t ). Inputs are current state y and current time t, output is the calculated derivative dydt.
• t0: initial time .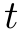
• dt: time step .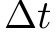

Returns: Initialized integrator object.

Properties:

• n: dimension of y0.
• y: current state. Initialized as a shallow copy of input y0.
• deriv: function that calculates the derivative. Initialized from input. May be changed.
• t: current time, incremented by dt with each time step.
• dt: time step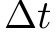 . Initialized from input dt. May be changed.

Methods:

• .step(): takes a single step of the RK-4 integrator and stores the result in-place in the y property.
• .steps( n ): takes n steps of the RK-4 integrator, storing the result in-place in the y property.

Credits

(c) 2015 Ricky Reusser. MIT License